Mbledhja dhe zbritja e Vektorёve. Metoda e koordinatave

I. Çfarё dimё tashmё pёr mbledhjen  dhe zbritjen e vektorёve

Siç dihet, vektor quhet segmenti i orientuar  nё tё cilin dallohet fillesa (origjina) dhe mbaresa (ekstrmiteti), Nё fig. 1, janё ndёrtuar vektorёt: 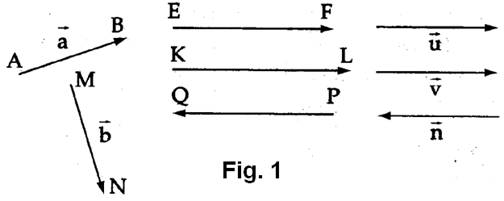 ku vektorёt kanё tё njёjtin drejtim (janё kolinearё; vektorёt kanё tё njёjtёn kahe ndёrsa vektorёt kanё kahe tё kundёrt  ().

Gjatёsia e vektorit ёshtё gjatёsia e segmentit, psh AB (shёnohet ).  Nё fig. 1, vihet re se vektorёt  kanё drejtime tё njёjta, kahe tё njёjta dhe gjatёsi tё barabarta. Ato quhen vektorё tё barabartё:  .. Vektorёt  kanё drejtime tё njёjta, kahe tё kundёrta dhe gjatёsi tё barabarta. Ato quhen vektorё tё kundёrt:  .

Shuma e dy vektorёve

a)  Rregulli i trekёndёshit

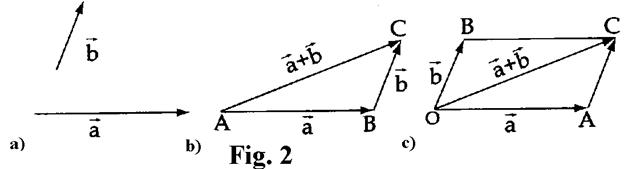Ky rregull tregohet nё fig. 2b. Pёr mbledhjen e vektorёve  (fig. 2 a)), veprojmё nё kёtё mёnyrё:

Zhvendosim vektorin  me fille;sё nё pikёn A, zhvendosim vektorin  me fillesё nё pikёn B , e cila ёshtё mbaresa e vektorit   (fig. 2 b)). Vektori  i cili ka pёr fillesё, fillesёn e vektorit tё parё  dhe pёr mbaresё, mbaresёn e vektorit tё dytё  , ёshtё shuma e vektorёve    dhe :

b) Rregulli i paralelogramit

I zhvendosim vektorёt  me fillesё nё tё njёtёn pikё O (fig. 2 c)) . Diagonalja  e paralelogramit OACB ёshtё shuma e vektorёve :

Mbledhja e vektorёve ka vetitё:

1.  (vetia e ndёrrrimit)

       2.    (vetia e shoqёrimit)

Shuma e disa vektorёve

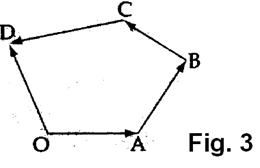
I vendosim vektorёt njeri pas tjetrit, nё mёnyrё qё mbaresa e vektorit tё parё tё pёrputhet me fillesёn e vektorit tё dytё, e kёshtu me rradhё. Vektori qё bashkon fillesёn e vektorit tё parё me mbaresёn e vektorit tё fundit quhet shumё e vektorёve tё dhёnё, Psh nё fig. 3, kemi: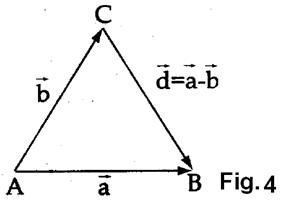

Diferenca e dy vektorёve

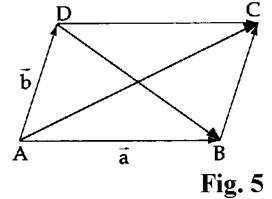
      Nga fig. 4, duket se diferenca e dy vektorёve ёshtё vektori , qё bashkon mbaresёn e vektorit tё dytё  me mbaresёn e vektorit tё parё  , Nё paralelogramin ABCD (fig. 5) , duket se diagonalja AC parqet shumёn e dy vektorёve , ndёrsa diagonalja DB paraqet diferencёn e vektorёve

II. Koordinatat e vektorit nё plan

Siç dihet, koordinatat e vektorit janё tё barabarta me diferencёn e koordinatave pёrkatёse tё mbaresёs dhe fillesёs sё tij. Psh. Nё fig. 6  ku kemi fillesёn M₁(x₁, y₁) dhe mbaresёn  M₂(x₂, y₂), vektori jepet nё koordinata: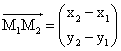

Shembull 1. Jepen pikat M(3, 2) dhe N(-1, 4). Tё gjenden koordinatat e vektorёve .

Zgjidhje:  . 

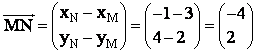    dhe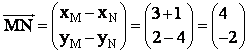          

Duket se vektorёt   janё tё kundёrt. Koordinatat e vektorёve tё kundёrt janё tё barabarta por me shenja  tё kundёrta, ndёrkohё qё vektorёt e njёjtё kanё koordinata tё barabarta nё madhёsi e nё shenjё.

Largesa ndёrmjet dy pikave. Gjatёsia e vektorit

Nga figura 6 duket largёsia midis dy pikave çfardo  nё plan: M₁(x₁, y₁) dhe M₂(x₂, y₂), gjendet nё bazё tё teoremёs sё Pitagorёs nga trekёndёshi kёndrejtё M₁PM₂ :

Njёkohёsisht, kjo forulё shpreh edhe gjatёsinё e vektorit 

III. Mbledhja dhe zbritja e vektorёve  nёpёrmjet koordinatave

Siç dihet, njё vektor çfardo nё plan,  mund tё paraqitet nёpёrmjet koordinatave qё janё diferenca e koordinatave tё skajeve tё tij. Psh vektori ,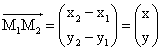

Nё njё sistem kordinativ xOy,  vektori mund tё parqitet edhe me pёrbёrset e tij sipas vektorёve njёsi  tё boshteve kordinative , pёrkatёsisisht Ox dhe Oy::

Ky quhet edhe zbёrthim i vektorit sipas vektorёve njёsi

Mbёshtetur nё kёtё zbёrthim, veprimet me vektorёt si mbledhja, zbritja, apo shumёzimi i vektorit me njё numёr, kryhen si nё shembullin mё  poshtё.:

Shembull:  Jepen vektrёt: 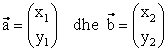 , tё gjenden

Zgjidhje

Vini re qё vektorёt   kanё drejtime tё njёjta. Nёse koordinatat e dy vektorёve janё tё pёrpjesshme, atёhere vektorёt kanё drejtim tё njёtё. ёshtё i vertetё edhe pohimi i anasjelltё.

Mbledhja dhe zbritja e vektorёve demonstrohen me anё tё applet-eve tё mёposhtme, ku vektorёt nuk janё shёnuar me shenjёn e shigjetёs sipёr simbolit tё tyre, por janё shёnuar thjeshtё A dhe B.